When A Polygon Reflects Across The Y-axis, How Do The Coordinates Of The Points Change?

What is a Reflection in Math?

Learning how to perform a reflection of a indicate, a line, or a figure across the ten axis or across the y axis is an important skill that every geometry math educatee must learn.

In real life, nosotros think of a reflection as a mirror image, like when we look at ain reflection in the mirror.

This idea of reflection correlating with a mirror image is similar in math.

This complete guide to reflecting over the ten axis and reflecting over the y axis will provide a stride-by-footstep tutorial on how to perform these translations.

Outset, let'south start with a reflection geometry definition:

Math Definition: Reflection Over the 10 Axis

A reflection of a indicate, a line, or a figure in the X axis involved reflecting the image over the ten axis to create a mirror epitome. In this instance, the ten axis would be called the axis of reflection.

Math Definition: Reflection Over the Y Centrality

A reflection of a point, a line, or a figure in the Y centrality involved reflecting the image over the Y centrality to create a mirror paradigm. In this case, theY centrality would be chosen the axis of reflection.

What is the dominion for a reflection beyond the X centrality?

The rule for reflecting over the Ten centrality is to negate the value of the y-coordinate of each point, merely leave the x-value the same.

For example, when point P with coordinates (v,iv) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,-4). Notice that the 10-coordinate for both points did not change, only the value of the y-coordinate changed from 4 to -4.

What is the dominion for a reflection across the Y centrality?

The dominion for reflecting over the Y axis is to negate the value of the x-coordinate of each point, but exit the -value the same.

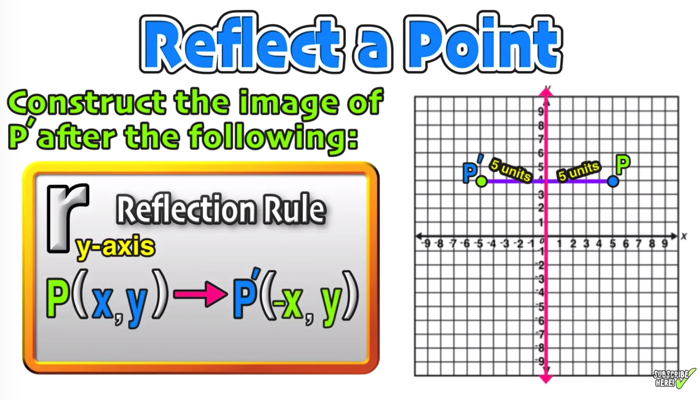
For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto betoken P', the coordinates of P' are (-5,4). Notice that the y-coordinate for both points did not change, but the value of the x-coordinate changed from 5 to -five.

You can think of reflections as a flip over a designated line of reflection. You tin can often visualize what a reflection over the x axis or a reflection over the y axis may look like before you ever apply whatsoever rules of plot any points. This aspect of reflections is helpful because you tin can often tell if your transformation is correct based on how information technology looks. If the new paradigm resembles a mirror image of the original, you're in proficient shape! If it does not, you probably did something wrong.

Examples of Reflection Over the X Axis and Y Axis:

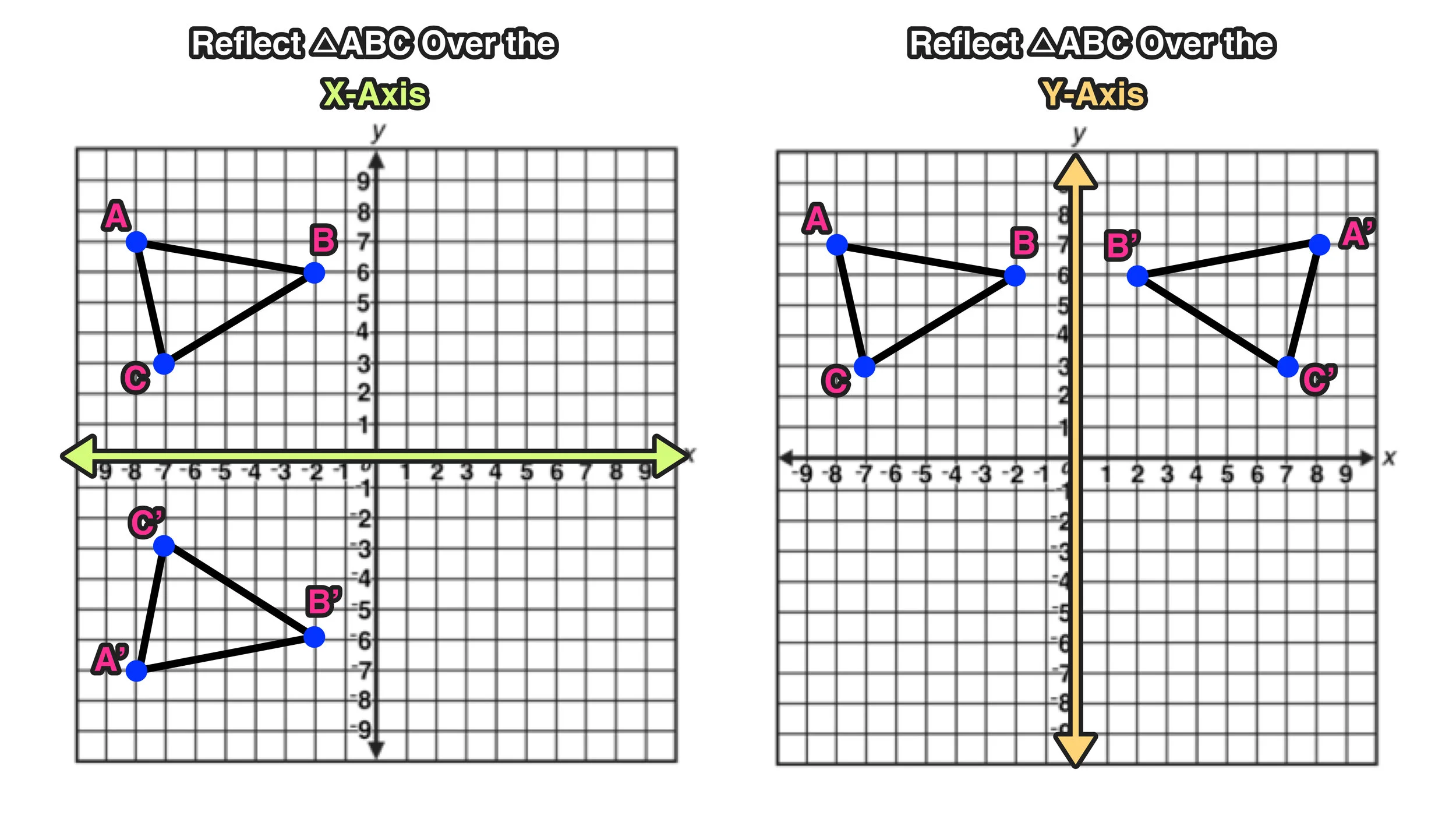
Notice how the reflection rules for reflecting across the x axis and across the y axis are applied in each instance.

Check out the video lesson beneath to larn more about reflections in geometry and for more free practice problems:

You can download the gratuitous lesson guide that accompanies this video lesson by clicking hither.

Looking for More Geometry Transformation Help?

Free Guide to Geometry Dilations and Calibration Factor

Free Guide to Rotations (ninety, 180, 270, 360)

Free Guide to Translations on the Coordinate Plane

Tags:Reflection over the x-axis (x axis), Reflection across the 10-centrality (ten axis), Reflection over the y-axis (y axis), Reflection beyond the y axis (y axis), Reflection in the x-centrality (ten axis), Reflection in the y axis,, Reflection geometry definition, Reflection math definition

Take thoughts? Share your thoughts in the comments department below!